背景
很多领域的很多问题,以及现实中的很多东西,都可以被建模为一个多元线性微分方程组。也就是说,一组变量随时间的变化率在任何时刻都由它们自身的线性组合决定。一般地,假设这组变量构成的向量是,我们可以找到一个方阵,使得
在此不推导求解过程,只给出如下结论:
为方便讨论,我们定义expm,expv。
设的维数是。现在,在通常数值精度的范围内计算expm最快的方式仍然需要的时间复杂度。但是通常,通过数值方法求解时,比起知道一个演化算符(即expm的结果),我们更关心一个具体的体系,在一个给定的初态下,将演化成什么样子,也就是求解expv。
成文时在一般条件下计算expv最快的方法仍然是Krylov子空间法。
何为Krylov子空间法?
熟悉数值计算的朋友们可能了解过共轭梯度CG优化算法等一系列其他问题上的Krylov子空间方法。其实Krylov子空间是一个比较泛的东西,他就是一个矩阵和一个向量在若干次矩阵乘法以内生成的线性空间。假设矩阵叫,向量叫,那么生成的阶Krylov子空间就是
其中 表示由集合中的向量任意线性组合生成的线性空间。若原来的空间有个维度,阶Krylov子空间则最多有个维度。通常情况下,我们设置的值将使远大于,从而使得在子空间里的计算是较廉价的。
Krylov子空间法,顾名思义,就是在这个子空间中尝试获得原问题的一个较好的近似。用数学的语言写出来,就是这样一个优化问题(在不作其他说明的情况下范数采用-范数):
当然,这个优化问题本身的求解也不是非常显然的。这是一个在比较奇怪的线性空间里约束的问题,我们先利用一组基展开,将它变成一个无约束优化问题。假设我们找到的一组基(基向量作为列向量拼成的矩阵),把表示成
那么原来的优化问题就变成了
看起来好像差不多,但是现在已经是一个常规的、无约束的最小二乘优化问题。我们知道,它的解是
其中表示的伪逆。但是解出来还不够,因为解里含有这个项,而这就是我们要求解的原问题。好像绕了一圈又绕回来了。其实不然。因为的维度原小于,我们可以并不需要计算,而尝试去用其他的办法获得它在上的投影。
这投影具体如何计算,就需要知道到底是什么。我们需要开始考虑给找一组计算上‘好用’的基了。
基
如果都不线性相关的话(如果它们线性相关,它其实是等价于一个更低阶的Krylov子空间,可以降到更小的m求解;而且可以证明对于随机选取的和,大概率它们是线性无关的),按照定义,就天然有一组基:
但是在数值上它有一些问题。对于大部分而言,会快速地收敛到的某个特征向量(每次归一化的话),换句话说,虽然在严格数学上这组天然的基是线性无关的,但是在计算机中,由于数值的精度有限,看起来这些基就好像线性相关了一样。
消除这种数值精度带来的线性相关也很简单,只需要使用线性代数课程上都会讲的史密定正交化,不记得的话可以搜索复习一下。一边生成这组基,一边进行正交化运算,这就是Arnoldi算法了。
Arnoldi:令,计算,随后对在上进行正交单位化;计算,随后对在上进行正交单位化……依次类推,直到个基向量都被找到。
通常我们需要做次矩阵-向量乘法,复杂度开销为。不过,如果矩阵具有稀疏性,或者有一些别的结构特性可以高效地计算这个矩阵-向量乘法的话可以更快。
求解EXPV
我们最终可以来计算了。
在刚才那组基下,由于我们进行了正交单位化处理,的伪逆实际上就是的共轭转置。我们记标准正交基下的第一个单位向量叫做,那么。我们再来表示:
当然,总是我们不想看到的东西。我们需要作一些近似。现在是先计算了这个演化算符,随后投影到子空间上。我们可以把整个算符投影到子空间里,随后再在子空间里进行演化。公式表达就是
是一个维的矩阵,采用通常的的方法就可以快速获得其expm。自身则在前面正交单位化的时候计算过了:正交单位化过程中计算了每个和前面所有的内积,而这就是这个矩阵。直观上,这就是把算符投影到子空间上之后所得到的结果。
这一步近似自然是有误差的。我们只是给出了一个直观的解释,详细的、严谨的分析需要使用Hermite插值多项式的相关理论,在这里只给出结论(可参考引文[1])。对于,近似的误差为
PS. 一些实际的考虑和小trick
可以看到,这里要求是比较小的。而实际遇到的可能比较大。我们可以把缩小一个倍数,随后多次应用这个方法近似,每次走一小步。在求解微分方程的时候,就是前文所说的每次选取一个较小的值、作多步计算。
实验结果展示
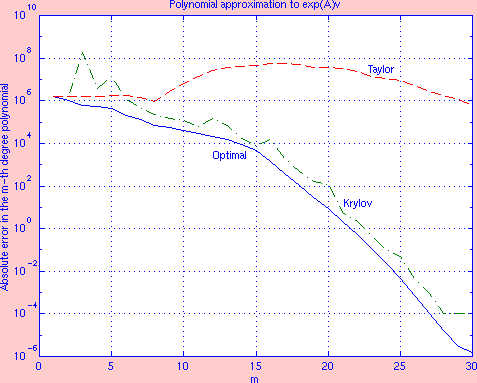
我们知道,矩阵e指数的定义就是用泰勒展开定义的。因此,随机生成一个中等规模的矩阵,将上述泰勒展开截断到项,和上述近似的Krylov子空间法、以及真实的子空间最优解(也就是先用的时间求expv再进行投影)进行比较。由于博主比较懒得跑实验,就贴一个别人文章里的图[2]。
参考
[1] Hochbruck, M., & Lubich, C. (1999). Exponential integrators for quantum-classical molecular dynamics. BIT Numerical Mathematics, 39(4), 620-645.
[2] Sidje, R. B. (1998). Expokit: A software package for computing matrix exponentials. ACM Transactions on Mathematical Software (TOMS), 24(1), 130-156.